Build procedural fluency from conceptual understanding is an essential component of mathematical education. By developing a deep understanding of mathematical concepts, students can develop the ability to apply procedures accurately and efficiently. This introduction explores the relationship between conceptual understanding and procedural fluency, providing a comprehensive overview of the topic.
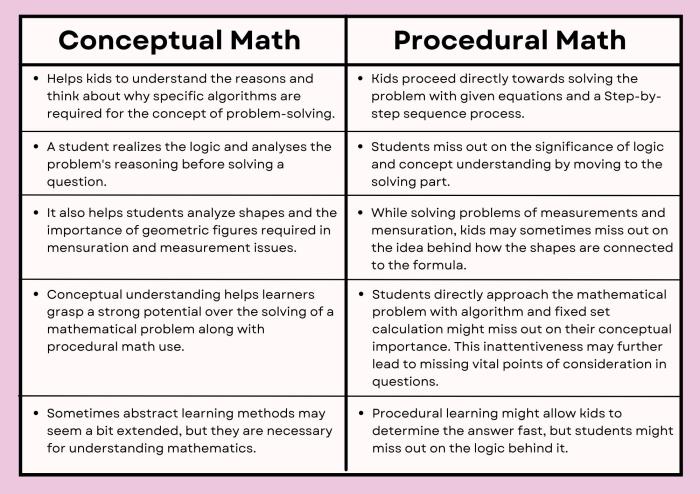
Conceptual understanding is the foundation upon which procedural fluency is built. When students have a strong conceptual understanding, they can make connections between different mathematical concepts and apply their knowledge to new situations. Procedural fluency, on the other hand, is the ability to perform mathematical procedures accurately and efficiently.
It involves the development of automaticity in carrying out mathematical operations.
1. Define Procedural Fluency: Build Procedural Fluency From Conceptual Understanding

Procedural fluency refers to the ability to execute mathematical procedures accurately, efficiently, and flexibly. It involves the mastery of algorithms and the ability to apply them in various contexts.
Importance of Procedural Fluency
- Enhances problem-solving abilities
- Supports deeper conceptual understanding
- Provides a foundation for higher-level mathematics
2. Conceptual Understanding and Procedural Fluency
Relationship Between Conceptual Understanding and Procedural Fluency, Build procedural fluency from conceptual understanding
Conceptual understanding and procedural fluency are intertwined. Conceptual understanding provides the foundation for procedural fluency, while procedural fluency reinforces and deepens conceptual understanding.
When students understand the underlying concepts behind a procedure, they can better apply it in different situations and make connections to other mathematical ideas.
3. Building Procedural Fluency from Conceptual Understanding
Effective Strategies
- Connect procedures to concepts:Explain the reasons behind each step in a procedure.
- Use models and manipulatives:Visual aids help students visualize and understand concepts.
- Provide multiple representations:Present concepts and procedures in different ways (e.g., symbols, diagrams, equations).
- Encourage student explanations:Have students explain their reasoning and the steps they take.
4. Examples of Procedural Fluency Activities
| Activity | Grade Level | Mathematical Concept |
|---|---|---|
| Number Bonds | K-2 | Addition and subtraction |
| Area and Perimeter Model Building | 3-5 | Geometry |
| Fraction Bars | 4-6 | Fractions |
| Algebra Tiles | 6-8 | Algebra |
5. Methods for Assessing Procedural Fluency
- Timed Tests:Measure speed and accuracy.
- Observation:Observe students applying procedures in real-world contexts.
- Interviews:Ask students to explain their reasoning and strategies.
- Problem-Solving Tasks:Assess students’ ability to apply procedures in novel situations.
6. Technology and Procedural Fluency

Role of Technology
Technology can enhance procedural fluency by providing:
- Interactive simulations and games
- Automated feedback and practice
- Personalized learning experiences
Examples include:
- Khan Academy
- IXL
- Math Playground
FAQ Explained
What is procedural fluency?
Procedural fluency is the ability to perform mathematical procedures accurately and efficiently.
How is conceptual understanding related to procedural fluency?
Conceptual understanding is the foundation upon which procedural fluency is built. When students have a strong conceptual understanding, they can make connections between different mathematical concepts and apply their knowledge to new situations.
Why is it important to build procedural fluency from conceptual understanding?
Building procedural fluency from conceptual understanding helps students develop a deep understanding of mathematical concepts and become proficient in performing mathematical procedures.